Category: Higher Ed

Making sense of noise: introducing students to stochastic processes in order to better understand biological behaviors (and even free will).

 Biological systems are characterized by the ubiquitous roles of weak, that is, non-covalent molecular interactions, small, often very small, numbers of specific molecules per cell, and Brownian motion. These combine to produce stochastic behaviors at all levels from the molecular and cellular to the behavioral. That said, students are rarely introduced to the ubiquitous role of stochastic processes in biological systems, and how they produce unpredictable behaviors. Here I present the case that they need to be and provide some suggestions as to how it might be approached.  

Background: Three recent events combined to spur this reflection on stochasticity in biological systems, how it is taught, and why it matters. The first was an article describing an approach to introducing students to homeostatic processes in the context of the bacterial lac operon (Booth et al., 2022), an adaptive gene regulatory system controlled in part by stochastic events. The second were in-class student responses to the question, why do interacting molecules “come back apart” (dissociate).  Finally, there is the increasing attention paid to what are presented as deterministic genetic factors, as illustrated by talk by Kathryn Harden, author of the “The Genetic Lottery: Why DNA matters for social equality” (Harden, 2021).  Previous work has suggested that students, and perhaps some instructors, find the ubiquity, functional roles, and implications of stochastic, that is inherently unpredictable processes, difficult to recognize and apply. Given their practical and philosophical implications, it seems essential to introduce students to stochasticity early in their educational journey.

added 7 March 2023; Should have cited:  You & Leu (2020).

What is stochasticity and why is it important for understanding biological systems? Stochasticity results when intrinsically unpredictable events, e.g. molecular collisions, impact the behavior of a system. There are a number of drivers of stochastic behaviors. Perhaps the most obvious, and certainly the most ubiquitous in biological systems is thermal motion. The many molecules within a solution (or a cell) are moving, they have kinetic energy – the energy of motion and mass. The exact momentum of each molecule cannot, however, be accurately and completely characterized without perturbing the system (echos of Heisenberg). Given the impossibility of completely characterizing the system, we are left uncertain as to the state of the system’s components, who is bound to whom, going forward. 

Through collisions energy is exchanged between molecules.  A number of chemical processes are driven by the energy delivered through such collisions. Think about a typical chemical reaction. In the course of the reaction, atoms are rearranged – bonds are broken (a process that requires energy) and bonds are formed (a process that releases energy). Many (most) of the chemical reactions that occur in biological systems require catalysts to bring their required activation energies into the range available within the cell.   [1]  

What makes the impact of thermal motion even more critical for biological systems is that many (most) regulatory interactions and macromolecular complexes, the molecular machines discussed by Alberts (1998) are based on relatively weak, non-covalent surface-surface interactions between or within molecules. Such interactions are central to most regulatory processes, from the activation of signaling pathways to the control of gene expression. The specificity and stability of these non-covalent interactions, which include those involved in determining the three-dimensional structure of macromolecules, are directly impacted by thermal motion, and so by temperature – one reason controlling body temperature is important.  

So why are these interactions stochastic and why does it matter?  A signature property of a stochastic process is that while it may be predictable when large numbers of atoms, molecules, or interactions are involved, the behaviors of individual atoms, molecules, and interactions are not. A classic example, arising from factors intrinsic to the atom, is the decay of radioactive isotopes. While the half-life of a large enough population of a radioactive isotope is well defined, when any particular atom will decay is, in current theory, unknowable, a concept difficult for students (see Hull and Hopf, 2020). This is the reason we cannot accurately predict whether Schrȍdinger’s cat is alive or dead. The same behavior applies to the binding of a regulatory protein to a specific site on a DNA molecule and its subsequent dissociation: predictable in large populations, not-predictable for individual molecules. The situation is exacerbated by the fact that biological systems are composed of cells and cells are, typically, small, and so contain relatively few molecules of each type (Milo and Phillips, 2015). There are typically one or two copies of each gene in a cell, and these may be different from one another (when heterozygous). The expression of any one gene depends upon the binding of specific proteins, transcription factors, that act to activate or repress gene expression. In contrast to a number of other cellular proteins, “as a rule of thumb, the concentrations of such transcription factors are in the nM range, corresponding to only 1-1000 copies per cell in bacteria or 103-106 in mammalian cells” (Milo and Phillips, 2015). Moreover, while DNA binding proteins bind to specific DNA sequences with high affinity, they also bind to DNA “non-specifically” in a largely sequence independent manner with low affinity. Given that there are many more non-specific (non-functional) binding sites in the DNA than functional ones, the effective concentration of a particular transcription factor can be significantly lower than its total cellular concentration would suggest. For example, in the case of the lac repressor of the bacterium Escherichia coli (discussed further below), there are estimated to be ~10 molecules of the tetrameric lac repressor per cell, but “non-specific affinity to the DNA causes >90% of LacI copies to be bound to the DNA at locations that are not the cognate promoter site” (Milo and Phillips, 2015); at most only a few molecules are free in the cytoplasm and available to bind to specific regulatory sites.  Such low affinity binding to DNA allows proteins to undergo one-dimensional diffusion, a process that can greatly speed up the time it takes for a DNA binding protein to “find” high affinity binding sites (Stanford et al., 2000; von Hippel and Berg, 1989). Most transcription factors bind in a functionally significant manner to hundreds to thousands of gene regulatory sites per cell, often with distinct binding affinities. The effective binding affinity can also be influenced by positive and negative interactions with other transcription and accessory factors, chromatin structure, and DNA modifications. Functional complexes can take time to assemble, and once assembled can initiate multiple rounds of polymerase binding and activation, leading to a stochastic phenomena known as transcriptional bursting. An analogous process occurs with RNA-dependent polypeptide synthesis (translation). The result, particularly for genes expressed at lower levels, is that stochastic (unpredictable) bursts of transcription/translation can lead to functionally significant changes in protein levels (Raj et al., 2010; Raj and van Oudenaarden, 2008).

Figure adapted from Elowitz et al 2002

There are many examples of stochastic behaviors in biological systems. Originally noted by Novick and Weiner (1957) in their studies of the lac operon, it was clear that gene expression occurred in an all or none manner. This effect was revealed in a particularly compelling manner by Elowitz et al (2002) who used lac operon promoter elements to drive expression of transgenes encoding cyan and yellow fluorescent proteins (on a single plasmid) in E. coli.  The observed behaviors were dramatic; genetically identical cells were found to express, stochastically, one, the other, both, or neither transgenes. The stochastic expression of genes and downstream effects appear to be the source of much of the variance found in organisms with the same genotype in the same environmental conditions (Honegger and de Bivort, 2018).

Beyond gene expression, the unpredictable effects of stochastic processes can be seen at all levels of biological organization, from the biased random walk behaviors that underlie various forms of chemotaxis (e.g. Spudich and Koshland, 1976) and the search behaviors in C. elegans (Roberts et al., 2016) and other animals (Smouse et al., 2010), the noisiness in the opening of individual neuronal voltage-gated ion channels (Braun, 2021; Neher and Sakmann, 1976), and various processes within the immune system (Hodgkin et al., 2014), to variations in the behavior of individual organisms (e.g. the leafhopper example cited by Honegger and de Bivort, 2018). Stochastic events are involved in a range of “social” processes in bacteria (Bassler and Losick, 2006). Their impact serves as a form of “bet-hedging” in populations that generate phenotypic variation in a homogeneous environment (see Symmons and Raj, 2016). Stochastic events can regulate the efficiency of replication-associated error-prone mutation repair (Uphoff et al., 2016) leading to increased variation in a population, particularly in response to environmental stresses. Stochastic “choices” made by cells can be seen as questions asked of the environment, the system’s response provides information that informs subsequent regulatory decisions (see Lyon, 2015) and the selective pressures on individuals in a population (Jablonka and Lamb, 2005). Together stochastic processes introduce a non-deterministic (i.e. unpredictable) element into higher order behaviors (Murakami et al., 2017; Roberts et al., 2016).

Controlling stochasticity: While stochasticity can be useful, it also needs to be controlled. Not surprisingly then there are a number of strategies for “noise-suppression”, ranging from altering regulatory factor concentrations, the formation of covalent disulfide bonds between or within polypeptides, and regulating the activity of repair systems associated with DNA replication, polypeptide folding, and protein assembly via molecular chaperones and targeted degradation. For example, the identification of “cellular competition” effects has revealed that “eccentric cells” (sometimes, and perhaps unfortunately referred to as of “losers”) can be induced to undergo apoptosis (die) or migration in response to their “normal” neighbors (Akieda et al., 2019; Di Gregorio et al., 2016; Ellis et al., 2019; Hashimoto and Sasaki, 2020; Lima et al., 2021).

Student understanding of stochastic processes: There is ample evidence that students (and perhaps some instructors as well) are confused by or uncertain about the role of thermal motion, that is the transfer of kinetic energy via collisions, and the resulting stochastic behaviors in biological systems. As an example, Champagne-Queloz et al (2016; 2017) found that few students, even after instruction through molecular biology courses, recognize that collisions with other molecules were  responsible for the disassembly of molecular complexes. In fact, many adopt a more “deterministic” model for molecular disassembly after instruction (see part A panel figure on next page). In earlier studies, we found evidence for a similar confusion among instructors (part B of figure on the next page)(Klymkowsky et al., 2010). 

Introducing stochasticity to students: Given that understanding stochastic (random) processes can be difficult for many (e.g. Garvin-Doxas and Klymkowsky, 2008; Taleb, 2005), the question facing course designers and instructors is when and how best to help students develop an appreciation for the ubiquity, specific roles, and implications of stochasticity-dependent processes at all levels in biological systems. I would suggest that  introducing students to the dynamics of non-covalent molecular interactions, prevalent in biological systems in the context of stochastic interactions (i.e. kinetic theory) rather than a ∆G-based approach may be useful. We can use the probability of garnering the energy needed to disrupt an interaction to present concepts of binding specificity (selectivity) and stability. Developing an understanding of the formation and  disassembly of molecular interactions builds on the same logic that Albert Einstein and Ludwig Böltzman used to demonstrate the existence of atoms and molecules and the reversibility of molecular reactions (Bernstein, 2006). Moreover, as noted by Samoilov et al (2006) “stochastic mechanisms open novel classes of regulatory, signaling, and organizational choices that can serve as efficient and effective biological solutions to problems that are more complex, less robust, or otherwise suboptimal to deal with in the context of purely deterministic systems.”

The selectivity (specificity) and stability of molecular interactions can be understood from an energetic perspective – comparing the enthalpic and entropic differences between bound and unbound states. What is often missing from such discussions, aside from the fact of their inherent complexity, particularly in terms of calculating changes in entropy and exactly what is meant by energy (Cooper and Klymkowsky, 2013) is that many students enter biology classes without a robust understanding of enthalpy, entropy, or free energy (Carson and Watson, 2002).  Presenting students with a molecular  collision, kinetic theory-based mechanism for the dissociation of molecular interactions, may help them better understand (and apply) both the dynamics and specificity of molecular interactions. We can gage the strength of an interaction (the sum of the forces stabilizing an interaction) based on the amount of energy (derived from collisions with other molecules) needed to disrupt it.  The implication of student responses to relevant Biology Concepts Instrument (BCI) questions and beSocratic activities (data not shown), as well as a number of studies in chemistry, is that few students consider the kinetic/vibrational energy delivered through collisions with other molecules (a function of temperature), as key to explaining why interactions break (see Carson and Watson, 2002 and references therein).  Although this paper is 20 years old, there is little or no evidence that the situation has improved. Moreover, there is evidence that the conventional focus on mathematics-centered, free energy calculations in the absence of conceptual understanding may serve as an unnecessary barrier to the inclusion of a more socioeconomically diverse, and under-served populations of students (Ralph et al., 2022; Stowe and Cooper, 2019). 

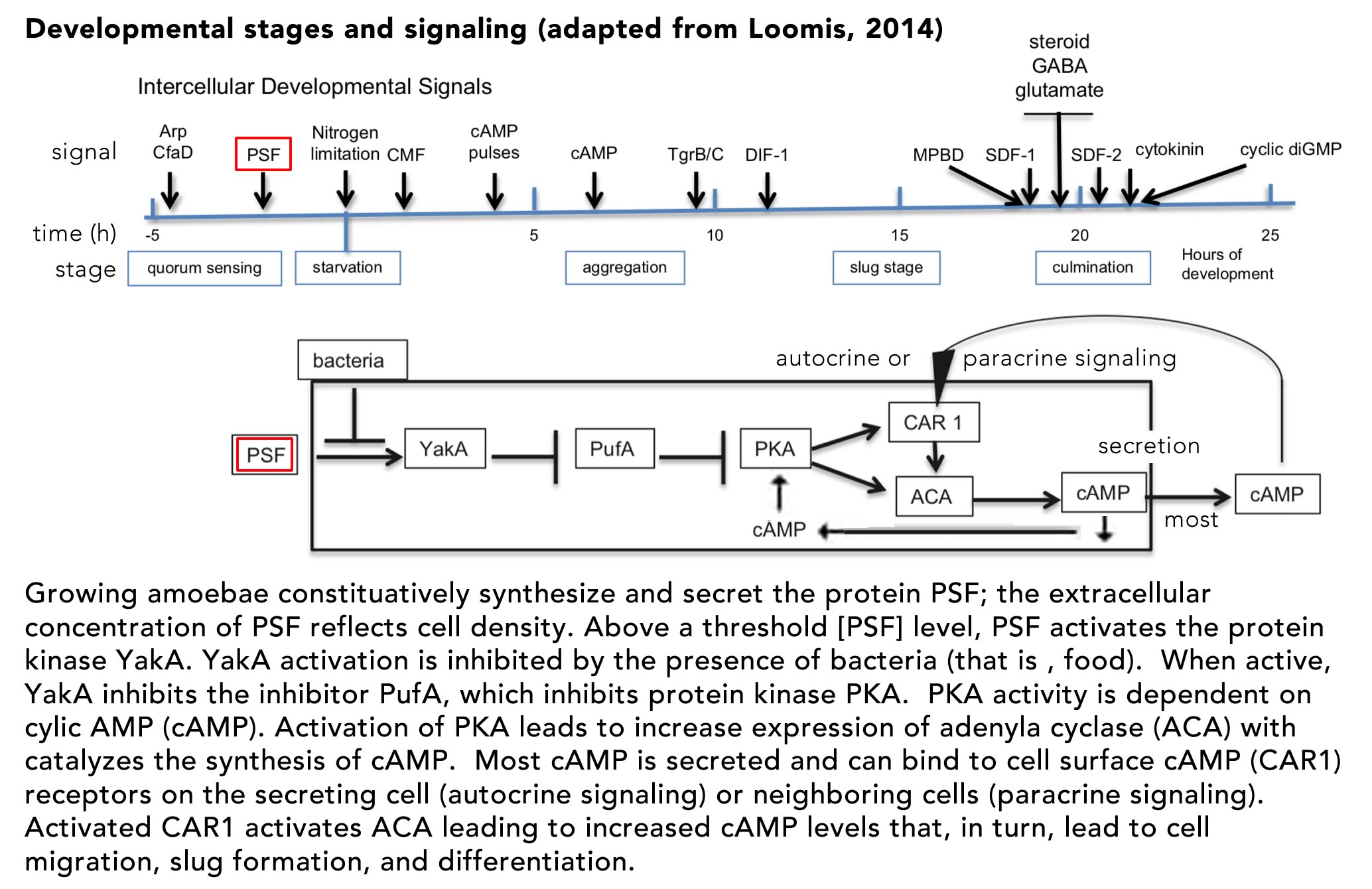
The lac operon as a context for introducing stochasticity: Studies of the E. coli  lac operon hold an iconic place in the history of molecular biology and are often found in introductory courses, although typically presented in a deterministic context. The mutational analysis of the lac operon helped define key elements involved in gene regulation (Jacob and Monod, 1961; Monod et al., 1963). Booth et al (2022) used the lac operon as the context for their “modeling and simulation lesson”, Advanced Concepts in Regulation of the Lac Operon. Given its inherently stochastic regulation (Choi et al., 2008; Elowitz et al., 2002; Novick and Weiner, 1957; Vilar et al., 2003), the lac operon is a good place to start introducing students to stochastic processes. In this light, it is worth noting that Booth et al describes the behavior of the lac operon as “leaky”, which would seem to imply a low, but continuous level of expression, much as a leaky faucet continues to drip. As this is a peer-reviewed lesson, it seems likely that it reflects widely held mis-understandings of how stochastic processes are introduced to, and understood by students and instructors.

E. coli cells respond to the presence of lactose in growth media in a biphasic manner, termed diauxie, due to “the inhibitory action of certain sugars, such as glucose, on adaptive enzymes (meaning an enzyme that appears only in the presence of its substrate)” (Blaiseau and Holmes, 2021). When these (preferred) sugars are depleted from the media, growth slows. If lactose is present, however, growth will resume following a delay associated with the expression of the proteins encoded by the operon that enables the cell to import and metabolize lactose. Although the term homeostatic is used repeatedly by Booth et al, the lac operon is part of an adaptive, rather than a homeostatic, system. In the absence of glucose, cyclic AMP (cAMP) levels in the cell rise. cAMP binds to and activates the catabolite activator protein (CAP), encoded for by the crp gene. Activation of CAP leads to the altered expression of a number of target genes, whose products are involved in adaption to the stress associated with the absence of common and preferred metabolites. cAMP-activated CAP acts as both a transcriptional repressor and activator, “and has been shown to regulate hundreds of genes in the E. coli genome, earning it the status of “global” or “master” regulator” (Frendorf et al., 2019). It is involved in the adaptation to environmental factors, rather than maintaining the cell in a particular state (homeostasis). 

The lac operon is a classic polycistronic bacterial gene, encoding three distinct polypeptides: lacZ (β-galactosidase), lacY (β-galactoside permease), and lacA (galactoside acetyltransferase). When glucose or other preferred energy sources are present, expression of the lac operon is blocked by the inactivity of CAP. The CAP protein is a homodimer and its binding to DNA is regulated by the binding of the allosteric effector cAMP.  cAMP is generated from ATP by the enzyme adenylate cyclase, encoded by the cya gene. In the absence of glucose the enyzme encoded by the crr gene is phosphorylated and acts to activate adenylate cyclase (Krin et al., 2002).  As cAMP levels increase, cAMP binds to the CAP protein, leading to a dramatic change in its structure (↑), such that the protein’s  DNA binding domain becomes available to interact with promoter sequences (figure from Sharma et al., 2009).

Binding of activated (cAMP-bound) CAP is not, by itself sufficient to activate expression of the lac operon because of the presence of the constitutively expressed lac repressor protein, encoded for by the lacI gene. The active repressor is a tetramer, present at very low levels (~10 molecules) per cell. The lac operon contains three repressor (“operator”) binding sites; the tetrameric repressor can bind two operator sites simultaneously (upper figure → from Palanthandalam-Madapusi and Goyal, 2011). In the absence of lactose, but in the presence of cAMP-activated CAP, the operon is expressed in discrete “bursts” (Novick and Weiner, 1957; Vilar et al., 2003). Choi et al (2008) found that these burst come in two types, short and long, with the size of the burst referring to the number of mRNA molecules synthesized (bottm figure adapted from Choi et al ↑). The difference between burst sizes arises from the length of time that the operon’s repressor binding sites are unoccupied by repressor. As noted above, the tetravalent repressor protein can bind to two operator sites at the same time. When released from one site, polymerase binding and initiation produces a small number of mRNA molecules. Persistent binding to the second site means that the repressor concentration remains locally high, favoring rapid rebinding to the operator and the cessation of transcription (RNA synthesis). When the repressor releases from both operator sites, a rarer event, it is free to diffuse away and interact (non-specifically, i.e. with low affinity) with other DNA sites in the cell, leaving the lac operator sites unoccupied for a longer period of time. The number of such non-specific binding sites greatly exceeds the number (three) of specific binding sites in the operon. The result is the synthesis of a larger “burst” (number) of mRNA molecules. The average length of time that the operator  sites remain unoccupied is a function of the small number of repressor molecules present and the repressor’s low but measurable non-sequence specific binding to DNA. 

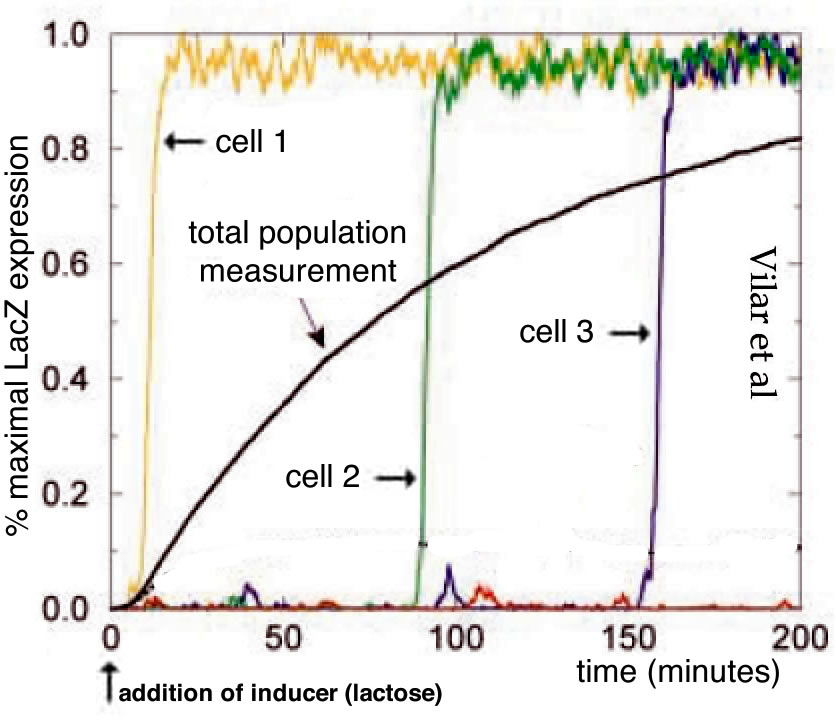
The expression of the lac operon leads to the appearance of β-galactosidase and β-galactoside permease. An integral membrane protein, β-galactoside permease enables extracellular lactose to enter the cell while cytoplasmic β-galactosidase catalyzes its breakdown and the generation of allolactone, which binds to the lac repressor protein, inhibiting its binding to operator sites, and so removing repression of transcription. In the absence of lactose, there are few if any of the proteins (β-galactosidase and β-galactoside permease) needed to activate the expression of the lac operon, so the obvious question is how, when lactose does appear in the extracellular media, does the lac operon turn on? Booth et al and the Wikipedia entry on the lac operon (accessed 29 June 2022) describe the turn on of the lac operon as “leaky” (see above). The molecular modeling studies of Vilar et al and Choi et al (which, together with Novick and Weiner, are not cited by Booth et al) indicate that the system displays distinct threshold and maintenance concentrations of lactose needed for stable lac gene expression. The term “threshold” does not occur in the Booth et al article. More importantly, when cultures are examined at the single cell level, what is observed is not a uniform increase in lac expression in all cells, as might be expected in the context of leaky expression, but more sporadic (noisy) behaviors. Increasing numbers of cells are “full on” in terms of lac operon expression over time when cultured in lactose concentrations above the operon’s activation threshold. This illustrates the distinctly different implications of a leaky versus a stochastic process in terms of their impacts on gene expression. While a leak is a macroscopic metaphor that produces a continuous, dependable, regular flow (drips), the occurrence of “bursts” of gene expression implies a stochastic (unpredictable) process ( figure from Vilar et al ↓). 

As the ubiquity and functionally significant roles of stochastic processes in biological systems becomes increasingly apparent, e.g. in the prediction of phenotypes from genotypes (Karavani et al., 2019; Mostafavi et al., 2020), helping students appreciate and understand the un-predictable, that is stochastic, aspects of biological systems becomes increasingly important. As an example, revealed dramatically through the application of single cell RNA sequencing studies, variations in gene expression between cells of the same “type” impacts organismic development and a range of behaviors. For example, in diploid eukaryotic cells is now apparent that in many cells, and for many genes, only one of the two alleles present is expressed; such “monoallelic” expression can impact a range of processes (Gendrel et al., 2014). Given that stochastic processes are often not well conveyed through conventional chemistry courses (Williams et al., 2015) or effectively integrated into, and built upon in molecular (and other) biology curricula; presenting them explicitly in introductory biology courses seems necessary and appropriate.

It may also help make sense of discussions of whether humans (and other organisms) have “free will”.  Clearly the situation is complex. From a scientific perspective we are analyzing systems without recourse to non-natural processes. At the same time, “Humans typically experience freely selecting between alternative courses of action” (Maoz et al., 2019)(Maoz et al., 2019a; see also Maoz et al., 2019b).  It seems possible that recognizing the intrinsically unpredictable nature of many biological processes (including those of the central nervous system) may lead us to conclude that whether or not free will exists is in fact a non-scientific, unanswerable (and perhaps largely meaningless) question. 

footnotes

[1]  For this discussion I will ignore entropy, a factor that figures in whether a particular reaction in favorable or unfavorable, that is whether, and the extent to which it occurs.  

Acknowledgements: Thanks to Melanie Cooper and Nick Galati for taking a look and Chhavinder Singh for getting it started. Updated 6 January 2023.

literature cited:

Akieda, Y., Ogamino, S., Furuie, H., Ishitani, S., Akiyoshi, R., Nogami, J., Masuda, T., Shimizu, N., Ohkawa, Y. and Ishitani, T. (2019). Cell competition corrects noisy Wnt morphogen gradients to achieve robust patterning in the zebrafish embryo. Nature communications 10, 1-17.

Alberts, B. (1998). The cell as a collection of protein machines: preparing the next generation of molecular biologists. Cell 92, 291-294.

Bassler, B. L. and Losick, R. (2006). Bacterially speaking. Cell 125, 237-246.

Bernstein, J. (2006). Einstein and the existence of atoms. American journal of physics 74, 863-872.

Blaiseau, P. L. and Holmes, A. M. (2021). Diauxic inhibition: Jacques Monod’s Ignored Work. Journal of the History of Biology 54, 175-196.

Booth, C. S., Crowther, A., Helikar, R., Luong, T., Howell, M. E., Couch, B. A., Roston, R. L., van Dijk, K. and Helikar, T. (2022). Teaching Advanced Concepts in Regulation of the Lac Operon With Modeling and Simulation. CourseSource.

Braun, H. A. (2021). Stochasticity Versus Determinacy in Neurobiology: From Ion Channels to the Question of the “Free Will”. Frontiers in Systems Neuroscience 15, 39.

Carson, E. M. and Watson, J. R. (2002). Undergraduate students’ understandings of entropy and Gibbs free energy. University Chemistry Education 6, 4-12.

Champagne-Queloz, A. (2016). Biological thinking: insights into the misconceptions in biology maintained by Gymnasium students and undergraduates”. In Institute of Molecular Systems Biology. Zurich, Switzerland: ETH Zürich.

Champagne-Queloz, A., Klymkowsky, M. W., Stern, E., Hafen, E. and Köhler, K. (2017). Diagnostic of students’ misconceptions using the Biological Concepts Instrument (BCI): A method for conducting an educational needs assessment. PloS one 12, e0176906.

Choi, P. J., Cai, L., Frieda, K. and Xie, X. S. (2008). A stochastic single-molecule event triggers phenotype switching of a bacterial cell. Science 322, 442-446.

Coop, G. and Przeworski, M. (2022). Lottery, luck, or legacy. A review of “The Genetic Lottery: Why DNA matters for social equality”. Evolution 76, 846-853.

Cooper, M. M. and Klymkowsky, M. W. (2013). The trouble with chemical energy: why understanding bond energies requires an interdisciplinary systems approach. CBE Life Sci Educ 12, 306-312.

Di Gregorio, A., Bowling, S. and Rodriguez, T. A. (2016). Cell competition and its role in the regulation of cell fitness from development to cancer. Developmental cell 38, 621-634.

Ellis, S. J., Gomez, N. C., Levorse, J., Mertz, A. F., Ge, Y. and Fuchs, E. (2019). Distinct modes of cell competition shape mammalian tissue morphogenesis. Nature 569, 497.

Elowitz, M. B., Levine, A. J., Siggia, E. D. and Swain, P. S. (2002). Stochastic gene expression in a single cell. Science 297, 1183-1186.

Feldman, M. W. and Riskin, J. (2022). Why Biology is not Destiny. In New York Review of Books. NY.

Frendorf, P. O., Lauritsen, I., Sekowska, A., Danchin, A. and Nørholm, M. H. (2019). Mutations in the global transcription factor CRP/CAP: insights from experimental evolution and deep sequencing. Computational and structural biotechnology journal 17, 730-736.

Garvin-Doxas, K. and Klymkowsky, M. W. (2008). Understanding Randomness and its impact on Student Learning: Lessons from the Biology Concept Inventory (BCI). Life Science Education 7, 227-233.

Gendrel, A.-V., Attia, M., Chen, C.-J., Diabangouaya, P., Servant, N., Barillot, E. and Heard, E. (2014). Developmental dynamics and disease potential of random monoallelic gene expression. Developmental cell 28, 366-380.

Harden, K. P. (2021). The genetic lottery: why DNA matters for social equality: Princeton University Press.

Hashimoto, M. and Sasaki, H. (2020). Cell competition controls differentiation in mouse embryos and stem cells. Current Opinion in Cell Biology 67, 1-8.

Hodgkin, P. D., Dowling, M. R. and Duffy, K. R. (2014). Why the immune system takes its chances with randomness. Nature Reviews Immunology 14, 711-711.

Honegger, K. and de Bivort, B. (2018). Stochasticity, individuality and behavior. Current Biology 28, R8-R12.

Hull, M. M. and Hopf, M. (2020). Student understanding of emergent aspects of radioactivity. International Journal of Physics & Chemistry Education 12, 19-33.

Jablonka, E. and Lamb, M. J. (2005). Evolution in four dimensions: genetic, epigenetic, behavioral, and symbolic variation in the history of life. Cambridge: MIT press.

Jacob, F. and Monod, J. (1961). Genetic regulatory mechanisms in the synthesis of proteins. Journal of molecular biology 3, 318-356.

Karavani, E., Zuk, O., Zeevi, D., Barzilai, N., Stefanis, N. C., Hatzimanolis, A., Smyrnis, N., Avramopoulos, D., Kruglyak, L. and Atzmon, G. (2019). Screening human embryos for polygenic traits has limited utility. Cell 179, 1424-1435. e1428.

Klymkowsky, M. W., Kohler, K. and Cooper, M. M. (2016). Diagnostic assessments of student thinking about stochastic processes. In bioArXiv: http://biorxiv.org/content/early/2016/05/20/053991.

Klymkowsky, M. W., Underwood, S. M. and Garvin-Doxas, K. (2010). Biological Concepts Instrument (BCI): A diagnostic tool for revealing student thinking. In arXiv: Cornell University Library.

Krin, E., Sismeiro, O., Danchin, A. and Bertin, P. N. (2002). The regulation of Enzyme IIAGlc expression controls adenylate cyclase activity in Escherichia coli. Microbiology 148, 1553-1559.

Lima, A., Lubatti, G., Burgstaller, J., Hu, D., Green, A., Di Gregorio, A., Zawadzki, T., Pernaute, B., Mahammadov, E. and Montero, S. P. (2021). Cell competition acts as a purifying selection to eliminate cells with mitochondrial defects during early mouse development. bioRxiv, 2020.2001. 2015.900613.

Lyon, P. (2015). The cognitive cell: bacterial behavior reconsidered. Frontiers in microbiology 6, 264.

Maoz, U., Sita, K. R., Van Boxtel, J. J. and Mudrik, L. (2019a). Does it matter whether you or your brain did it? An empirical investigation of the influence of the double subject fallacy on moral responsibility judgments. Frontiers in Psychology 10, 950.

Maoz, U., Yaffe, G., Koch, C. and Mudrik, L. (2019b). Neural precursors of decisions that matter—an ERP study of deliberate and arbitrary choice. Elife 8, e39787.

Milo, R. and Phillips, R. (2015). Cell biology by the numbers: Garland Science.

Monod, J., Changeux, J.-P. and Jacob, F. (1963). Allosteric proteins and cellular control systems. Journal of molecular biology 6, 306-329.

Mostafavi, H., Harpak, A., Agarwal, I., Conley, D., Pritchard, J. K. and Przeworski, M. (2020). Variable prediction accuracy of polygenic scores within an ancestry group. Elife 9, e48376.

Murakami, M., Shteingart, H., Loewenstein, Y. and Mainen, Z. F. (2017). Distinct sources of deterministic and stochastic components of action timing decisions in rodent frontal cortex. Neuron 94, 908-919. e907.

Neher, E. and Sakmann, B. (1976). Single-channel currents recorded from membrane of denervated frog muscle fibres. Nature 260, 799-802.

Novick, A. and Weiner, M. (1957). Enzyme induction as an all-or-none phenomenon. Proceedings of the National Academy of Sciences 43, 553-566.

Palanthandalam-Madapusi, H. J. and Goyal, S. (2011). Robust estimation of nonlinear constitutive law from static equilibrium data for modeling the mechanics of DNA. Automatica 47, 1175-1182.

Raj, A., Rifkin, S. A., Andersen, E. and van Oudenaarden, A. (2010). Variability in gene expression underlies incomplete penetrance. Nature 463, 913-918.

Raj, A. and van Oudenaarden, A. (2008). Nature, nurture, or chance: stochastic gene expression and its consequences. Cell 135, 216-226.

Ralph, V., Scharlott, L. J., Schafer, A., Deshaye, M. Y., Becker, N. M. and Stowe, R. L. (2022). Advancing Equity in STEM: The Impact Assessment Design Has on Who Succeeds in Undergraduate Introductory Chemistry. JACS Au.

Roberts, W. M., Augustine, S. B., Lawton, K. J., Lindsay, T. H., Thiele, T. R., Izquierdo, E. J., Faumont, S., Lindsay, R. A., Britton, M. C. and Pokala, N. (2016). A stochastic neuronal model predicts random search behaviors at multiple spatial scales in C. elegans. Elife 5, e12572.

Samoilov, M. S., Price, G. and Arkin, A. P. (2006). From fluctuations to phenotypes: the physiology of noise. Science’s STKE 2006, re17-re17.

Sharma, H., Yu, S., Kong, J., Wang, J. and Steitz, T. A. (2009). Structure of apo-CAP reveals that large conformational changes are necessary for DNA binding. Proceedings of the National Academy of Sciences 106, 16604-16609.

Smouse, P. E., Focardi, S., Moorcroft, P. R., Kie, J. G., Forester, J. D. and Morales, J. M. (2010). Stochastic modelling of animal movement. Philosophical Transactions of the Royal Society B: Biological Sciences 365, 2201-2211.

Spudich, J. L. and Koshland, D. E., Jr. (1976). Non-genetic individuality: chance in the single cell. Nature 262, 467-471.

Stanford, N. P., Szczelkun, M. D., Marko, J. F. and Halford, S. E. (2000). One-and three-dimensional pathways for proteins to reach specific DNA sites. The EMBO Journal 19, 6546-6557.

Stowe, R. L. and Cooper, M. M. (2019). Assessment in Chemistry Education. Israel Journal of Chemistry.

Symmons, O. and Raj, A. (2016). What’s Luck Got to Do with It: Single Cells, Multiple Fates, and Biological Nondeterminism. Molecular cell 62, 788-802.

Taleb, N. N. (2005). Fooled by Randomness: The hidden role of chance in life and in the markets. (2nd edn). New York: Random House.

Uphoff, S., Lord, N. D., Okumus, B., Potvin-Trottier, L., Sherratt, D. J. and Paulsson, J. (2016). Stochastic activation of a DNA damage response causes cell-to-cell mutation rate variation. Science 351, 1094-1097.

You, Shu-Ting, and Jun-Yi Leu. “Making sense of noise.” Evolutionary Biology—A Transdisciplinary Approach(2020): 379-391.

Vilar, J. M., Guet, C. C. and Leibler, S. (2003). Modeling network dynamics: the lac operon, a case study. J Cell Biol 161, 471-476.

von Hippel, P. H. and Berg, O. G. (1989). Facilitated target location in biological systems. Journal of Biological Chemistry 264, 675-678.

Williams, L. C., Underwood, S. M., Klymkowsky, M. W. and Cooper, M. M. (2015). Are Noncovalent Interactions an Achilles Heel in Chemistry Education? A Comparison of Instructional Approaches. Journal of Chemical Education 92, 1979–1987.

 

Higher Education Malpractice: curving grades

If there is one thing that university faculty and administrators could do today to demonstrate their commitment to inclusion, not to mention teaching and learning over sorting and status, it would be to ban curve-based, norm-referenced grading. Many obstacles exist to the effective inclusion and success of students from underrepresented (and underserved) groups in science and related programs.  Students and faculty often, and often correctly, perceive large introductory classes as “weed out” courses preferentially impacting underrepresented students. In the life sciences, many of these courses are “out-of-major” requirements, in which students find themselves taught with relatively little regard to the course’s relevance to bio-medical careers and interests. Often such out-of-major requirements spring not from a thoughtful decision by faculty as to their necessity, but because they are prerequisites for post-graduation admission to medical or graduate school. “In-major” instructors may not even explicitly incorporate or depend upon the materials taught in these out-0f-major courses – rare is the undergraduate molecular biology degree program that actually calls on students to use calculus or a working knowledge of physics, despite the fact that such skills may be relevant in certain biological contexts – see Magnetofiction – A Reader’s Guide.  At the same time, those teaching “out of major” courses may overlook the fact that many (and sometimes most) of their students are non-chemistry, non-physics, and/or non-math majors.  The result is that those teaching such classes fail to offer a doorway into the subject matter to any but those already comfortable with it. But reconsidering the design and relevance of these courses is no simple matter.  Banning grading on a curve, on the other  hand, can be implemented overnight (and by fiat if necessary). 

 So why ban grading on a curve?  First and foremost, it would put faculty and institutions on record as valuing student learning outcomes (perhaps the best measure of effective teaching) over the sorting of students into easy-to-judge groups.  Second, there simply is no pedagogical justification for curved grading, with the possible exception of providing a kludgy fix to correct for poorly designed examinations and courses. There are more than enough opportunities to sort students based on their motivation, talent, ambition, “grit,” and through the opportunities they seek after and successfully embraced (e.g., through volunteerism, internships, and independent study projects). 

The negative impact of curving can be seen in a recent paper by Harris et al,  (Reducing achievement gaps in undergraduate general chemistry …), who report a significant difference in overall student inclusion and subsequent success based on a small grade difference between a C, which allows a student to proceed with their studies (generally as successfully as those with higher grades) and a C-minus, which requires them to retake the course before proceeding (often driving them out of the major).  Because Harris et al., analyzed curved courses, a subset of students cannot escape these effects.  And poor grades disproportionately impact underrepresented and underserved groups – they say explicitly “you do not belong” rather than “how can I help you learn”.   

Often naysayers disparage efforts to improve course design as “dumbing down” the course, rather than improving it.  In many ways this is a situation analogous to blaming patients for getting sick or not responding to treatment, rather than conducting an objective analysis of the efficacy of the treatment.  If medical practitioners had maintained this attitude, we would still be bleeding patients and accepting that more than a third are fated to die, rather than seeking effective treatments tailored to patients’ actual diseases – the basis of evidence-based medicine.  We would have failed to develop antibiotics and vaccines – indeed, we would never have sought them out. Curving grades implies that course design and delivery are already optimal, and the fate of students is predetermined because only a percentage can possibly learn the material.  It is, in an important sense, complacent quackery.

Banning grading on a curve, and labelling it for what it is – educational malpractice – would also change the dynamics of the classroom and might even foster an appreciation that a good teacher is one with the highest percentage of successful students, e.g. those who are retained in a degree program and graduate in a timely manner (hopefully within four years). Of course, such an alternative evaluation of teaching would reflect a department’s commitment to construct and deliver the most engaging, relevant, and effective educational program. Institutional resources might even be used to help departments generate more objective, instructor-independent evaluations of learning outcomes, in part to replace the current practice of student-based opinion surveys, which are often little more than measures of popularity.  We might even see a revolution in which departments compete with one another to maximize student inclusion, retention, and outcomes (perhaps even to the extent of applying pressure on the design and delivery of “out of major” required courses offered by other departments).  

“All a pipe dream” you might say, but the available data demonstrates that resources spent on rethinking course design, including engagement and relevance, can have significant effects on grades, retention, time to degree, and graduation rates.  At the risk of being labeled as self-promoting, I offer the following to illustrate the possibilities: working with Melanie Cooper at Michigan State University, we have built such courses in general and organic chemistry and documented their impact, see Evaluating the extent of a large-scale transformation in gateway science courses.

Perhaps we should be encouraging students to seek out legal representation to hold institutions (and instructors) accountable for detrimental practices, such as grading on a curve.  There might even come a time when professors and departments would find it prudent to purchase malpractice insurance if they insist on retaining and charging students for ineffective educational strategies.(1)  

Acknowledgements: Thanks to daughter Rebecca who provided edits and legal references and Melanie Cooper who inspired the idea. Educate! image from the Dorian De Long Arts & Music Scholarship site.

(1) One cannot help but wonder if such conduct could ever rise to the level of fraud. See, e.g., Bristol Bay Productions, LLC vs. Lampack, 312 P.3d 1155, 1160 (Colo. 2013) (“We have typically stated that a plaintiff seeking to prevail on a fraud claim must establish five elements: (1) that the defendant made a false representation of a material fact; (2) that the one making the representation knew it was false; (3) that the person to whom the representation was made was ignorant of the falsity; (4) that the representation was made with the intention that it be acted upon; and (5) that the reliance resulted in damage to the plaintiff.”).

Going virtual without a net

Is the coronavirus-based transition from face to face to on-line instruction yet another step to down-grading instructional quality?

transitioning education overnight

It is certainly a strange time in the world of higher education. In response to the current corona virus pandemic, many institutions have quickly, sometimes within hours and primarily by fiat, transitioned from face to face to distance (web-based) instruction. After a little confusion, it appears that laboratory courses are included as well, which certainly makes sense. While virtual laboratories can be built (see our own virtual laboratories in biology)  they typically fail to capture the social setting of a real laboratory.  More to the point, I know of no published studies that have measured the efficacy of such on-line experiences in terms of the ideas and skills students master.

Many instructors (including this one) are being called upon to carry out a radical transformation of instructional practice “on the fly.” Advice is being offered from all sides, from University administrators and technical advisors (see as an example Making Online Teaching a Success).  It is worth noting that much (all?) of this advice falls into the category of “personal empiricism”, suggestions based on various experiences but unsupported  by objective measures of educational outcomes – outcomes that include the extent of student engagement as well as clear descriptions of i) what students are expected to have mastered, ii) what they are expected to be able to do with their knowledge, and iii) what they can actually do. Again, to my knowledge there have been few if any careful comparative studies on learning outcomes achieved via face to face versus virtual teaching experiences. Part of the issue is that many studies on teaching strategies (including recent work on what has been termed “active learning” approaches) have failed to clearly define what exactly is to be learned, a necessary first step in evaluating their efficacy.  Are we talking memorization and recognition, or the ability to identify and apply core and discipline-specific ideas appropriately in novel and complex situations?

At the same time, instructors have not had practical training in using available tools (zoom, in my case) and little in the way of effective support. Even more importantly, there are few published and verified studies to inform what works best in terms of student engagement and learning outcomes. Even if there were clear “rules of thumb” in place to guide the instructor or course designer, there has not been the time or resources needed to implement these changes. The situation is not surprising given that the quality of university level educational programs rarely attracts critical analysis, or the necessary encouragement, support, and recognition needed to make it a departmental priority (see Making education matter in higher education).  It seems to me that the current situation is not unlike attempting to perform a complicated surgery after being told to watch a 3 minute youtube video. Unsurprisingly patient (student learning) outcomes may not be pretty.     

Much of what is missing from on-line instructional scenarios is the human connection, the ability of an instructor to pay attention to how students respond to the ideas presented. Typically this involves reading the facial expressions and body language of students, and through asking challenging (Socratic) questions – questions that address how the information presented can be used to generate plausible explanations or to predict the behavior of a system. These are interactions that are difficult, if not impossible to capture in an on-line setting.

While there is much to be said for active engagement/active learning strategies (see Hake 1998, Freeman et al 2014 and Theobald et al 2020), one can easily argue that all effective learning scenarios involve an instructor who is aware and responsive to students’ pre-existing knowledge. It is also important that the instructor has the willingness (and freedom) to entertain their questions, confusions, and the need for clarification (saying it a different way), or when it may be necessary to revisit important, foundational, ideas and skills – a situation that can necessitate discarding planned materials and “coaching up” students on core concepts and their application. The ability of the instructor to customize instruction “on the fly” is one of the justifications for hiring disciplinary experts in instructional positions, they (presumably) understand the conceptual foundations of the materials they are called upon to present. In its best (Socratic) form, the dialog between student and instructor drives students (and instructors) to develop a more sophisticated and metacognitive understanding of the web of ideas involved in most scientific explanations.

In the absence of an explicit appreciation of the importance of the human interactions between instructor and student, interactions already strained in the context of large enrollment courses, we are likely to find an increase in the forces driving instruction to become more and more about rote knowledge, rather than the higher order skills associated with the ability to juggle ideas, identifying those needed and those irrelevant to a specific situation.  While I have been trying to be less cynical (not a particularly easy task in the modern world), I suspect that the flurry of advice on how to carry out distance learning is more about avoiding the need to refund student fees than about improving students’ educational outcomes (see Colleges Sent Students Home. Now Will They Refund Tuition?)

A short post-script (17 April 2020): Over the last few weeks I have put together the tools to make the on-line MCDB 4650 Developmental Biology course somewhat smoother for me (and hopefully the students). I use Keynote (rather than Powerpoint) for slides; since the iPad is connected wirelessly to the project, this enables me to wander around the class room. The iOS version of Keynote enables me, and students, to draw on slides. Now that I am tethered, I rely more on pre-class beSocratic activities and the Mirroring360 application to connect my iPad to my laptop for Zoom sessions. I am back to being more interactive with the materials presented. I am also starting to pick students at random to answer questions & provide explanations (since they are quiet otherwise) – hopefully that works. Below (↓) is my set up, including a good microphone, laptop, iPad, and the newly arrived volume on Active Learning.

Gradients & Molecular Switches: a biofundamentalist perspective

Embryogenesis is based on a framework of social (cell-cell) interactions, initial and early asymmetries, and cascading cell-cell signaling and gene regulatory networks (DEVO posts one, two, & three). The result is the generation of embryonic axes, germ layers (ectoderm, mesoderm, endoderm), various organs and tissues (brains, limbs, kidneys, hearts, and such) and their characteristic cell types, their patterning, and their coordination into a functioning organism. It is well established that all animals share a common ancestor (hundreds of millions of years ago) and that a number of molecular  modules were already present in that common ancestor.  

At the same time evolutionary processes are, and need to be, flexible enough to generate the great diversity of organisms, with their various adaptations to particular life-styles. The extent of both conservation and flexibility (new genes, new mechanisms) in developmental systems is, however, surprising. Perhaps the most striking evidence for the depth of this conservation was supplied by the discovery of the organization of the Hox gene cluster in the fruit fly Drosophila and in the mouse (and other vertebrates). In both, the Hox genes are arranged and expressed in a common genomic and expression patterns. But as noted by Denis Duboule (2007) Hox gene organization is often presented in textbooks in a distorted manner (↓).

hox gene cluster variation

The Hox gene clusters of vertebrates are compact, but are split, disorganized, and even “atomized” in other types of organisms. Similarly, processes that might appear foundational, such as the role of the Bicoid gradient in the early fruit fly embryo (a standard topic in developmental biology textbooks), is in fact restricted to a small subset of flies (Stauber et al., 1999). New genes can be generated through well defined processes, such as gene duplication and divergence, or they can arise de novo out of sequence noise (Carvunis et al., 2012; Zhao et al., 2014 – see Van Oss & Carvunis 2019. De novo gene birth). Comparative genomic analyses can reveal the origins of specific adaptations (see Stauber et al., 1999).  The result is that organisms as closely related to each other as the great apes (including humans) have significant species-specific genetic differences (see Florio et al., 2018; McLean et al., 2011; Sassa, 2013 and references therein) as well as common molecular and cellular mechanisms.

A universal (?) feature of developing systems – gradients and non-linear responses: There is a predilection to find (and even more to teach) simple mechanisms that attempt to explain everything (witness the distortion of the Hox cluster, above) – a form of physics “theory of everything” envy.  But the historic nature, evolutionary plasticity, and need for regulatory robustness generally lead to complex and idiosyncratic responses in biological systems.  Biological systems are not “intelligently designed” but rather cobbled together over time through noise (mutation) and selection (Jacob, 1977)(see blog post). 
That said, a  common (universal?) developmental process appears to be the transformation of asymmetries into unambiguous cell fate decisions. Such responses are based on threshold events controlled by a range of molecular behaviors, leading to discrete gene expression states. We can approach the question of how such decisions are made from both an abstract and a concrete perspective. Here I outline my initial approach – I plan to introduce organism specific details as needed.  I start with the response to a signaling gradient, such as that found in many developmental systems, including the vertebrate spinal cord (top image Briscoe and Small, 2015) and the early Drosophila embryo (Lipshitz, 2009)(↓). gradients-decisions

bicoid gradient - lipschitz

We begin with a gradient in the concentration of a “regulatory molecule” (the regulator).  The shape of the gradient depends upon the sites and rates of synthesis, transport away from these sites, and turnover (degradation and/or inactivation). We assume, for simplicity’s sake, that the regulator directly controls the expression of target gene(s). Such a molecule binds in a sequence specific manner to regulatory sites, there could be a few or hundreds, and lead to the activation (or inhibition) of the DNA-dependent, RNA polymerase (polymerase), which generates RNA molecules complementary to one strand of the DNA. Both the binding of the regulator and the polymerase are stochastic processes, driven by diffusion, molecular collisions, and binding interactions.(1) 

Let us now consider the response of target gene(s) as a function of cell position within the gradient.  We might (naively) expect that the rate of target gene expression would be a simple function of regulator concentration. For an activator, where the gradient is high, target gene expression would be high, where the gradient concentration is low, target gene expression would be low – in between, target gene expression would be proportional to regulator concentration.  But generally we find something different, we find that the expression of target genes is non-uniform, that is there are thresholds in the gradient: on one side of the threshold concentration the target gene is completely off (not expressed), while on the other side of the threshold concentration, the target gene is fully on (maximally expressed).  The target gene responds as if it is controlled by an on-off switch. How do we understand the molecular basis for this behavior? 

Distinct mechanisms are used in different systems, but we will consider a system from the gastrointestinal bacteria E. coli that students may already be familiar with; these are the genes that enable E. coli to digest the mammalian milk sugar lactose.  They encode a protein needed to import  lactose into a bacterial cell and an enzyme needed to break lactose down so that it can be metabolized.  Given the energetic cost to synthesize these proteins, it is in the bacterium’s adaptive self interest to synthesize them only when lactose is present at sufficient concentrations in their environment.  The response is functionally similar to that associated with quorum sensing, which is also governed by threshold effects. Similarly cells respond to the concentration of regulator molecules (in a gradient) by turning on specific genes in specific domains, rather than uniformly. 

Now let us look in a little more detail at the behavior of the lactose utilization system in E. coli following an analysis by Vilar et al (2003)(2).  At an extracellular lactose concentration below the threshold, the system is off.  If we increase the extracellular lactose concentration above threshold the system turns on, the lactose permease and β-galactosidase proteins are made and lactose can enter the cell and be broken down to produce metabolizable sugars.  By looking at individual cells, we find that they transition, apparently stochastically from off to on (→), but whether they stay on depends upon the extracellular lactose concentration. We can define a concentration, the maintenance concentration, below the threshold, at which “on” cells will remain on, while “off” cells will remain off.  

The circuitry of the lactose system is well defined  (Jacob and Monod, 1961; Lewis, 2013; Monod et al., 1963)(↓).  The lacI gene encodes the lactose operon repressor protein and it is expressed constituately at a low level; it binds to sequences in the lac operon and inhibits transcription.  The lac operon itself contains three genes whose expression is regulated by a constituatively active promoter.  LacY encodes the permease while the lacZ encodes β-galactosidase.  β-galactosidase has two functions: it catalyzes the reaction that transforms lactose into allolactone and it cleaves lactose into the metabolically useful sugars glucose and galactose. Allolactone is an allosteric modulator of the Lac repressor protein; if allolactone is present, it binds to lac epressor proteins and inactivates them, allowing lac operon expression.  

The cell normally contains only ~10 lactose repressor proteins. Periodically (stochastically), even in the absence of lactose, and so its derivative allolactone, the lac operon promoter region is free of repressor proteins, and a lactose operon is briefly expressed – a few LacY and LacZ  polypeptides are synthesized (↓).  This noisy leakiness in the regulation of the lac operon allows the cell to respond if lactose happens to be present – some lactose molecules enter the cell through the permease, are converted to allolactone by β-galactosidase.  Allolactone is an allosteric effector of the lac repressor; when present it binds to and inactivates the lac repressor protein so that it no longer binds to its target sequences (the operator or “O” sites).  In the absence of repressor binding, the lac operon is expressed.  If lactose is not present, the lac operon is inhibited and lacY and LacZ disappear from the cell by turnover or growth associated dilution.     

The question of how the threshold concentration for various signal-regulated decisions is set often involves homeostatic processes that oppose the signaling response. The binding and activation of regulators can involve cooperative interactions between molecular components and both positive and negative feedback effects. 

In the case of patterning a tissue, in terms of regional responses to a signaling gradient, there can be multiple regulatory thresholds for different genes, as well as indirect effects, where the initiation of gene expression of one set of target genes impacts the sensitive expression of subsequent sets of genes.  One widely noted mechanism, known as reaction-diffusion, was suggested by the English mathematician Alan Turing (see Kondo and Miura, 2010) – it postulates a two component system. One component is an activator of gene expression, which in addition to its own various targets, positively regulates its own expression. The second component is a repressor of the first.  Both of these two regulator molecules are released by the signaling cell or cells; the repressor diffuses away from the source faster than the activator does.  The result can be a domain of target gene expression (where the concentration of activator is sufficient to escape repression), surrounded by a zone in which expression is inhibited (where repressor concentration is sufficient to inhibit the activator).  Depending upon the geometry of the system, this can result in discrete regions (dots or stripes) of primary target gene expression  (see Sheth et al., 2012).  In real systems there are often multiple gradients present; their relative orientations can produce a range of patterns.   

The point of all of this, is that when we approach a particular system – we need to consider the mechanisms involved.  Typically they are selected to produce desired phenotypes, but also to be robust in the sense that they need to produce the same patterns even if the system in which they occur is subject to perturbations, such as embryo/tissue size (due to differences in cell division / growth rates) and temperature and other environmental variables. 

note: figures returned – updated 13 November 2020.  

Footnotes:

  1. While stochastic (random) these processes can still be predictable.  A classic example involves the decay of an unstable isotope (atom), which is predictable at the population level, but unpredictable at the level of an individual atom.  Similarly, in biological systems, the binding and unbinding of molecules to one another, such as a protein transcription regulator to its target DNA sequence is stochastic but can be predictable in a large enough population.   
  2. and presented in biofundamentals ( pages 216-218). 

literature cited: 

Briscoe & Small (2015). Morphogen rules: design principles of gradient-mediated embryo patterning. Development 142, 3996-4009.

Carvunis et al  (2012). Proto-genes and de novo gene birth. Nature 487, 370.

Duboule (2007). The rise and fall of Hox gene clusters. Development 134, 2549-2560.

Florio et al (2018). Evolution and cell-type specificity of human-specific genes preferentially expressed in progenitors of fetal neocortex. eLife 7.

Jacob  (1977). Evolution and tinkering. Science 196, 1161-1166.

Jacob & Monod (1961). Genetic regulatory mechanisms in the synthesis of proteins. Journal of Molecular Biology 3, 318-356.

Kondo & Miura (2010). Reaction-diffusion model as a framework for understanding biological pattern formation. Science 329, 1616-1620.

Lewis (2013). Allostery and the lac Operon. Journal of Molecular Biology 425, 2309-2316.

Lipshitz (2009). Follow the mRNA: a new model for Bicoid gradient formation. Nature Reviews Molecular Cell Biology 10, 509.

McLean et al  (2011). Human-specific loss of regulatory DNA and the evolution of human-specific traits. Nature 471, 216-219.

Monod Changeux & Jacob (1963). Allosteric proteins and cellular control systems. Journal of Molecular Biology 6, 306-329.

Sassa (2013). The role of human-specific gene duplications during brain development and evolution. Journal of Neurogenetics 27, 86-96.

Sheth et al (2012). Hox genes regulate digit patterning by controlling the wavelength of a Turing-type mechanism. Science 338, 1476-1480.

Stauber et al (1999). The anterior determinant bicoid of Drosophila is a derived Hox class 3 gene. Proceedings of the National Academy of Sciences 96, 3786-3789.

Vilar et al (2003). Modeling network dynamics: the lac operon, a case study. J Cell Biol 161, 471-476.

Zhao et al (2014). Origin and Spread of de Novo Genes in Drosophila melanogaster Populations. Science. 343, 769-772

Aggregative & clonal metazoans: a biofundamentalist perspective

21st Century DEVO-2  In the first post in this series [link], I introduced the observation that single celled organisms can change their behaviors, often in response to social signals.  They can respond to changing environments and can differentiate from one cellular state to the another. Differentiation involves changes in which sets of genes are expressed, which polypeptides and proteins are made [previous post], where the proteins end up within the cell, and which behaviors are displayed by the organism. Differentiation enables individuals to adapt to hostile conditions and to exploit various opportunities. 

The ability of individuals to cooperate with one another, through processes such as quorum sensing, enables them to tune their responses so that they are appropriate and useful. Social interactions also makes it possible for them to produce behaviors that would be difficult or impossible for isolated individuals.  Once individual organisms learn, evolutionarily, how to cooperate, new opportunities and challenges (cheaters) emerge. There are strategies that can enable an organism to adapt to a wider range of environments, or to become highly specialized to a specific environment,  through the production of increasingly complex behaviors.  As described previously, many of these cooperative strategies can be adopted by single celled organisms, but others require a level of multicellularity.  Multicellularity can be transient – a pragmatic response to specific conditions, or it can be (if we ignore the short time that gametes exist as single cells) permanent, allowing the organism to develop the range of specialized cells types needed to build large, macroscopic organisms with complex and coordinated behaviors. In appears that various forms of multicellularity have arisen independently in a range of lineages (Bonner, 1998; Knoll, 2011). We can divide multicellularity into two distinct types, aggregative and clonal – which we will discuss in turn (1).  Aggregative (transient) multicellularity:  Once organisms had developed quorum sensing, they can monitor the density of related organisms in their environment and turn or (or off) specific genes (or sets of genes, necessary to produce a specific behavior.  While there are many variants, one model for such  a behavior is  a genetic toggle switch, in which a particular gene (or genes) can be switched on or off in response to environmental signals acting as allosteric regulators of transcription factor proteins (see Gardner et al., 2000).  Here is an example of an activity (↓) that we will consider in class to assess our understanding of the molecular processes involved.

One outcome of such a signaling system is to provoke the directional migration of amoeba and their aggregation to form the transient multicellular “slug”.  Such behaviors has been observed  in a range of normally unicellular organisms (see Hillmann et al., 2018)(↓). The classic example is  the cellular slime mold Dictyostelium discoideum (Loomis, 2014).  Under normal conditions, these

unicellular amoeboid eukaryotes migrate, eating bacteria and such. In this state, the range of an individual’s movement is restricted to short distances.  However when conditions turn hostile, specifically a lack of necessary nitrogen compounds, there is a compelling reason to abandon one environment and migrate to another, more distant that a single-celled organism could reach. This is a behavior that depends upon the presence of a sufficient density (cells/unit volume) of cells that enables them to: 1) recognize one another’s presence (through quorum sensing), 2) find each other through directed (chemotactic) migration, and 3) form a multicellular slug that can go on to differentiate. Upon differentiation about 20% of the cells differentiate (and die), forming a stalk that lifts the other ~80% of the cells into the air.  These non-stalk cells (the survivors) differentiate into spore (resistant to drying out) cells that are released into the air where they can be carried to new locations, establishing new populations.  

The process of cellular differentiation in D. discoideum has been worked out in molecular detail and involves two distinct signaling systems: the secreted pre-starvation factor (PSF) protein and cyclic AMP (cAMP).  PSF is a quorum signaling protein that also serves to activate the cell aggregation and differentiation program (FIG. ↓)

If bacteria, that is food, are present, the activity of PSF is inhibited and  cells remain in their single cell state. The key regulator of downstream aggregation and differentiation is the cAMP-dependent protein kinase PKA.  In the unicellular state, PKA activity is inhibited by PufA.  As PSF increases, while food levels decrease, YakA activity increases, inactivating PufA, leading to increased PKA activity.  Active PKA induces the synthesis of two downstream proteins, adenylate cyclase (ACA) and the cAMP receptor (CAR1). ACA catalyzes cAMP synthesis, much of which is secreted from the cell as a signaling molecule. The membrane-bound CAR1 protein acts as a receptor for autocrine (on the cAMP secreting cell) and paracrine (on neighboring cells) signaling.  The binding of cAMP to CAR1 leads to further activation of PKA, increasing cAMP synthesis and secretion – a positive feed-back loop. As cAMP levels increase, downstream genes are activated (and inhibited) leading cells to migrate toward one another, their adhesion to form a slug.  Once the slug forms and migrates to an appropriate site, the process of differentiation (and death) leading to stalk and spore formation begins. The fates of the aggregated cells is determined stochastically, but social cheaters can arise. Mutations can lead to individuals that avoid becoming stalk cells.  In the long run, if all individuals were to become cheaters, it would be impossible to form a stalk, so the purpose of social cooperation would be impossible to achieve.  In the face of environmental variation, populations invaded by cheaters are more likely to become extinct.  For our purposes the various defenses against cheaters are best left to other courses (see here if interested Strassmann et al., 2000).  

Clonal (permanent) multicellularity:  The type of multicellularity that most developmental biology courses focus on is what is termed clonal multicellularity – the organism is a clone of an original cell, the zygote, a diploid cell produced by the fusion of sperm and egg, haploid cells formed through the process of meiosis (2).  It is during meiosis that most basic genetic processes occur, that is the recombination between maternal and paternal chromosomes leading to the shuffling of alleles along a chromosome, and the independent segregation of chromosomes to form haploid gametes, gametes that are genetically distinct from those present in either parent. Once the zygote forms, subsequent cell divisions involve mitosis, with only a subset of differentiated cells, the cells of the germ line, capable of entering meiosis.  

Non-germ line, that is somatic cells, grow and divide. They interact with one another directly and through various signaling processes to produce cells with distinct patterns of gene expression, and so differentiated behaviors.  A key difference from a unicellular organism, is that the cells will (largely) stay attached to one another, or to extracellular matrix materials secreted by themselves and their neighbors.  The result is ensembles of cells displaying different specializations and behaviors.  As such cellular colonies get larger, they face a number of physical constraints – for example, cells are open non-equilibrium systems, to maintain themselves and to grow and reproduce, they need to import matter and energy from the external world. Cells also produce a range of, often toxic, waste products that need to be removed.  As the cluster of zygote-derived cells grows larger, and includes more and more cells, some cells will become internal and so cut off from necessary resources. While diffusive processes are often adequate when a cell is bathed in an aqueous solution, they are inadequate for a cell in the interior of a large cell aggregate (3).  The limits of diffusive processes necessitate other strategies for resource delivery and waste removal; this includes the formation of tubular vascular systems (such as capillaries, arteries, veins) and contractile systems (hearts and such) to pump fluids through these vessels, as well as cells specialized to process and transport a range of nutrients (such as blood cells).  As organisms get larger, their movements require contractile machines (muscle, cartilage, tendons, bones, etc) driving tails, fins, legs, wings, etc. The coordination of such motile systems involves neurons, ganglia, and brains. There is also a need to establish barriers between the insides of an organism and the outside world (skin, pulmonary, and gastrointestinal linings) and the need to protect the interior environment from invading pathogens (the immune system).  The process of developing these various systems depends upon controlling patterns of cell growth, division, and specialization (consider the formation of an arm), as well as the controlled elimination of cells (apoptosis), important in morphogenesis (forming fingers from paddle-shaped appendages), the maturation of the immune system (eliminating cells that react against self), and the wiring up, and adaptation of the nervous system. Such changes are analogous to those involved in aggregative multicellularity.      

Origins of multicellularity:  While aggregative multicellularity involves an extension of quorum sensing and social cooperation between genetically distinct, but related individuals, we can wonder whether similar drivers are responsible for clonal multicellularity.  There are a number of imaginable adaptive (evolutionary) drivers but two spring to mind: a way to avoid predators by getting bigger than the predators and as a way to produce varied structures needed to exploit various ecological niches and life styles. An example of the first type of driver of multicellularity is offered by the studies of Boraas et al  (1998). They cultured the unicellular green alga Chlorella vulgaris, together with a unicellular predator, the phagotrophic flagellated protist Ochromonas vallescia. After less than 100 generations (cell divisions), they observed the appearance of multicellular, and presumable inedible (or at least less easily edible), forms. Once selected, this trait appears to be stable, such that “colonies retained the eight-celled form indefinitely in continuous culture”.  To my knowledge, the genetic basis for this multicellularity remains to be determined.  

Cell Differentiation:  One feature of simple colonial organisms is that when dissociated into individual cells, each cell is capable of regenerating a new organism. The presence of multiple (closely related) cells in a single colony opens up the possibility of social interactions; this is distinct from the case in aggregative multicellularity, where social cooperation came first. Social cooperation within a clonal metazoan means that most cells “give up” their ability to reproduce a new organism (a process involving meiosis). Such irreversible social interactions mark the transition from a colonial organism to a true multicellular organism. As social integration increases, cells can differentiate so as to perform increasingly specialized functions, functions incompatible with cell division. Think for a moment about a human neuron or skeletal muscle cell – in both cases, cell division is no longer possible (apparently). Nevertheless, the normal functioning of such cells enhances the reproductive success of the organism as a whole – a classic example of inclusive fitness (remember heterocysts?)  Modern techniques of single cell sequencing and data analysis have now been employed to map this process of cellular differentiation in increasingly great detail, observations that will inform our later discussions (see Briggs et al., 2018 and future posts). In contrast, the unregulated growth of a cancer cell is an example of an asocial behavior, an asocial behavior that is ultimately futile, except in those rare cases (four known at this point) in which a cancer cell can move from one organism to another (Ujvari et al., 2016).  

Unicellular affordances for multicellularity:  When considering the design of a developmental biology course, we are faced with the diversity of living organisms – the basic observation that Darwin, Wallace, their progenitors and disciplinary descendants set out to solve. After all there are many millions of different types of organisms; among the multicellular eukaryotes, there are six major group : the ascomycetes and basidiomycetes fungi, the florideophyte red algae, laminarialean brown algae, embryophytic land plants and animals

(Knoll, 2011 ↑).  Our focus will be on animals. “All members of Animalia are multicellular, and all are heterotrophs (i.e., they rely directly or indirectly on other organisms for their nourishment). Most ingest food and digest it in an internal cavity.” [Mayer link].  From a macroscopic perspective, most animals have (or had at one time during their development) an anterior to posterior, that is head to tail, axis. Those that can crawl, swim, walk, or fly typically have a dorsal-ventral or back to belly axis, and some have a left-right axis as well.  

But to be clear, a discussion of the various types of animals is well beyond the scope of any introductory course in developmental biology, in part because there are 35 (assuming no more are discovered) different “types” (phyla) of animals – nicely illustrated at this website [BBC: 35 types of animals, most of whom are really weird)].  So again, our primary focus will be on one group, the vertebrates – humans are members of this group.  We will also consider experimental insights derived from studies of various “model” systems, including organisms from another metazoan group, the  ecdysozoa (organisms that shed their outer layer as they grow bigger), a group that includes fruit flies and nematode worms. 

My goal will be to ignore most of the specialized terminology found in the scholarly literature, which can rapidly turn a biology course into a vocabulary lesson and that add little to understanding of basic processes relevant to a general understanding of developmental processes (and relevant to human biology, medicine, and biotechnology). This approach is made possible by the discovery that the basic processes associated with animal (and metazoan) development are conserved. In this light, no observation has been more impactful than the discovery that the nature and organization of the genes involved in specifying the head to tail axes of the fruit fly and vertebrates (such as the mouse and human) is extremely similar in terms of genomic organization and function (Lappin et al., 2006 ↓), an observation that we will return to repeatedly.  Such molecular similarities extend to cell-cell and cell-matrix adhesion systems, systems that release and respond to various signaling molecules, controlling cell behavior and gene expression, and reflects the evolutionary conservation and the common ancestry of all animals (Brunet and King, 2017; Knoll, 2011). 

What can we know about the common ancestor of the animals?  Early on in the history of comparative cellular anatomy, the striking structural similarities between  the feeding system of choanoflagellate protozoans, a motile (microtubule-based) flagellum a surrounded by a “collar”of microfilament-based microvilli) and a structurally similar organelle in a range of multicellular organisms led to the suggestion that choanoflagellates and animals shared a common ancestor.  The advent of genomic sequencing and analysis has only strengthened this hypothesis, namely that choanoflagellates and animals form a unified evolutionary clade, the ‘Choanozoa’  (see tree↑ above)(Brunet and King, 2017).  Moreover, “many genes required for animal multicellularity (e.g., tyrosine kinases, cadherins, integrins, and extracellular matrix domains) evolved before animal origins”.  The implications is that the Choanozoan ancestor was predisposed to exploit some of the early opportunities offered by clonal multicellularity. These pre-existing affordances, together with newly arising genes and proteins (Long et al., 2013) were exploited in multiple lineages in the generation of multicellular organisms (see Knoll, 2011).

Basically to understand what happened next, some ~600 million years ago or so, we will approach the various processes involved in the shaping of animal development.  Because all types of developmental processes, including the unicellular to colonial transition, involve changes in gene expression, we will begin with the factors involved in the regulation of gene expression.  


Footnotes:
1). Please excuse the inclusive plural, but it seems appropriate in the context of what I hope will be a highly interactive course.
2). I will explicitly ignore variants as (largely) distractions, better suited for more highly specialized courses.
3). We will return to this problem when (late in the course, I think) we will discuss the properties of induced pluripotent stem cell (iPSC) derived organoids.

Literature cited:
Bonner, J. T. (1998). The origins of multicellularity. Integrative Biology: Issues, News, and Reviews: Published in Association with The Society for Integrative and Comparative Biology 1, 27-36.

Boraas, M. E., Seale, D. B. and Boxhorn, J. E. (1998). Phagotrophy by a flagellate selects for colonial prey: a possible origin of multicellularity. Evolutionary Ecology 12, 153-164.

Briggs, J. A., Weinreb, C., Wagner, D. E., Megason, S., Peshkin, L., Kirschner, M. W. and Klein, A. M. (2018). The dynamics of gene expression in vertebrate embryogenesis at single-cell resolution. Science 360, eaar5780.

Brunet, T. and King, N. (2017). The origin of animal multicellularity and cell differentiation. Developmental cell 43, 124-140.

Gardner, T. S., Cantor, C. R. and Collins, J. J. (2000). Construction of a genetic toggle switch in Escherichia coli. Nature 403, 339-342.

Hillmann, F., Forbes, G., Novohradská, S., Ferling, I., Riege, K., Groth, M., Westermann, M., Marz, M., Spaller, T. and Winckler, T. (2018). Multiple roots of fruiting body formation in Amoebozoa. Genome biology and evolution 10, 591-606.

Knoll, A. H. (2011). The multiple origins of complex multicellularity. Annual Review of Earth and Planetary Sciences 39, 217-239.

Lappin, T. R., Grier, D. G., Thompson, A. and Halliday, H. L. (2006). HOX genes: seductive science, mysterious mechanisms. The Ulster medical journal 75, 23.

Long, M., VanKuren, N. W., Chen, S. and Vibranovski, M. D. (2013). New gene evolution: little did we know. Annual review of genetics 47, 307-333.

Loomis, W. F. (2014). Cell signaling during development of Dictyostelium. Developmental biology 391, 1-16.

Strassmann, J. E., Zhu, Y. and Queller, D. C. (2000). Altruism and social cheating in the social amoeba Dictyostelium discoideum. Nature 408, 965-967.

Ujvari, B., Gatenby, R. A. and Thomas, F. (2016). Transmissible cancers, are they more common than thought? Evolutionary applications 9, 633-634.